Diagramas de venn

CONJUNTOS DIAGRAMA DE VENN 

PROPIEDADES...

CONJUNTO:En matemáticas, un conjunto es una colección de elementos con características similares considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas,números,colores, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:

P = {2, 3, 5, 7, 11, 13, )

DIAGRAMA DE VENN

Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matematicas, logica de clases y razonamiento dragmatico Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

Los diagramas de Venn fueron ideados hacia 1880 por John venn

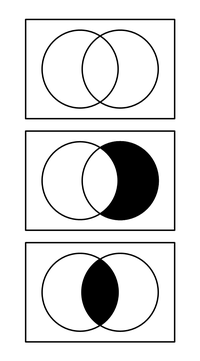
PROPIEDADES

Intersección

Dado que los conjuntos pueden tener elementos comunes, las regiones encerradas por sus líneas límite se superponen. El conjunto de los elementos que pertenecen simultáneamente a otros dos es la intersección de ambos.

Inclusión

Si todos los elementos de un conjunto son parte de los elementos de otro, se dice que el primero es un subconjunto del segundo o que está incluido en el segundo.¹​ En los diagramas de Venn, todas las regiones de superposición posibles deben ser representadas. Y, cuando hay regiones que no contienen elementos (regiones vacías), la situación se indica anulándolas (con un color de fondo distinto).²​

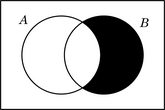
Disyunción

Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.