ECUACIONES Y DESIGUALDADES😃😁😂
Resolver Ecuaciones con Valores Absolutos😌😔😖😗
Como los valores positivos y negativos tienen un valor absoluto positivo, resolver ecuaciones con valores absolutos significa encontrar la solución para ambos valores positivo y negativo.
Primero veamos un ejemplo básico.
La ecuación dice “el valor absoluto de x es igual a cinco.” La solución es el valor o valores que estás a cinco unidades a partir de 0 en la recta numérica.
Podrías pensar inmediatamente en el 5; que es una solución de la ecuación. Observa que −5 también es una solución porque −5 está a 5 unidades del 0 en la dirección opuesta. Entonces la solución a la ecuación 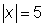 es x = −5 o x = 5.
es x = −5 o x = 5.
Un problema más complejo de valor absoluto se resuelve de manera similar. Considera 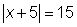 . Esta ecuación te pide encontrar qué número mas 5 tiene un valor absoluto de 15. Como 15 y −15 tienen valor absoluto de 15, la ecuación de valor absoluto es válida cuando la cantidad x + 5 es 15 o x + 5 es −15, ya que |15| = 15 y |−15| = 15. Entonces, necesitas encontrar qué valor de x hará la expresión igual a 15 así como qué valor de x hará la expresión igual a −15. Resolviendo las dos ecuaciones obtienes:
. Esta ecuación te pide encontrar qué número mas 5 tiene un valor absoluto de 15. Como 15 y −15 tienen valor absoluto de 15, la ecuación de valor absoluto es válida cuando la cantidad x + 5 es 15 o x + 5 es −15, ya que |15| = 15 y |−15| = 15. Entonces, necesitas encontrar qué valor de x hará la expresión igual a 15 así como qué valor de x hará la expresión igual a −15. Resolviendo las dos ecuaciones obtienes:
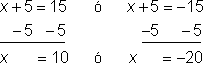
Puedes comprobar ambas soluciones en la ecuación de valor absoluto para ver si x = 10 y x = −20 son correctos.
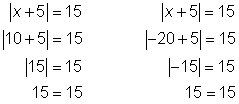
Resolver Ecuaciones de la Forma |x| = a
Para cualquier número positivo a, la solución de |x| = a es
x = a o x = −a
x puede ser una variable o una expresión algebraica.
|
Veamos otro ejemplo.
Ejemplo
| ||||
Problema
|
Resolver p.
|2p – 4| = 26
| |||
Escribe las dos ecuaciones que te darán un valor absoluto de 26.
| ||||
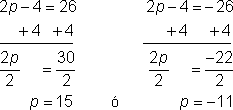 |
Resuelve cada ecuación para p despejando la variable.
| |||
Comprobar | 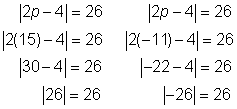 |
Comprueba las soluciones en la ecuación original.
¡Ambas soluciones funcionan!
| ||
Respuesta
| ||||
Algunas veces, tienes que despejar el valor absoluto antes de resolver la ecuación. Un ejemplo se muestra abajo.
Ejemplo
| |||||
Problema
|
Resolver w.
3|4w – 1| – 5 = 10
| ||||
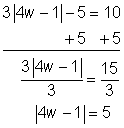 |
Despeja el término con el valor absoluto sumando 5 a ambos lados.
Divide ambos lados entre 3.
Ahora el valor absoluto está despejado.
| ||||
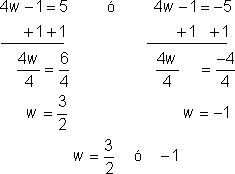 |
Escribe las dos ecuaciones que te darán un valor absoluto de 5 y resuélvelas.
| ||||
Comprobar
| 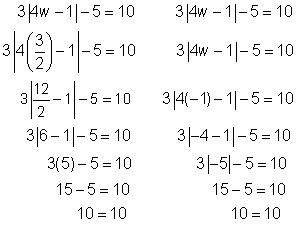 |
Comprueba las soluciones en la ecuación original.
¡Ambas soluciones funcionan!
| |||
Respuesta
| |||||
Veamos otro ejemplo:
Resolver y.
Antes de eliminar el signo de valor absoluto y hacer dos ecuaciones, piensa en lo que significa la ecuación. Dice “el valor absoluto de la cantidad 3y menos 5 es igual a −1.” Recuerda que un valor absoluto es la distancia de 0 en la recta numérica, entonces debe ser un número positivo, Como es imposible tener un valor absoluto igual a −1, esta ecuación no tiene solución. No existen valores de y que hagan un enunciado válido. No hay nada que hacer además de saber que la ecuación no tiene soluciones.
Apliquemos lo que ya sabes sobre resolver ecuaciones que contienen valores absolutos y lo que sabes sobre desigualdades para resolver desigualdades que contienen valores absolutos. Empecemos con una desigualdad simple.
La desigualdad dice, “el valor absoluto de x es menor o igual a 4.” Si se te pide resolver x, quieres encontrar los valores de x que están a 4 unidades o menos de 0 en la recta numérica. Podrías empezar imaginando la recta numérica y los valores de x que satisfacen esta ecuación.
4 y −4 están a cuatro unidades del 0, entonces son soluciones. 3 y −3 también son soluciones porque cada uno de estos valores está a menos de cuatro unidades del 0. Al igual que el 1 y el −1, el 0.5 y el −0.5, etc. — hay un número infinito de valores de x que satisfacen la desigualdad.
La gráfica de esta desigualdad tendrá dos círculos cerrados, en 4 y en −4. La distancia entre estos dos círculos en la recta numérica está coloreada de azul porque estos son los valores que satisfacen la ecuación.

La solución se puede escribir de esta manera: −4 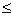 x
x 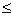 4.
4.
La situación es un poco distinta cuando el signo de desigualdad es “mayor que” o “mayor o igual a.” Considera la desigualdad simple 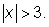 También, podrías pensar en la recta numérica y los valores de x mayores de tres unidades a partir del 0. Esta vez, 3 y −3 no están incluidos en la solución, entonces hay dos círculos abiertos en estos valores. 2 y −2 no serían soluciones porque no están a más de tres unidades del 0. Pero 5 y −5 si están y también lo están todos los valores extendiéndose a la izquierda de −3 y a la derecha de 3. La gráfica se vería como la que está abajo.
También, podrías pensar en la recta numérica y los valores de x mayores de tres unidades a partir del 0. Esta vez, 3 y −3 no están incluidos en la solución, entonces hay dos círculos abiertos en estos valores. 2 y −2 no serían soluciones porque no están a más de tres unidades del 0. Pero 5 y −5 si están y también lo están todos los valores extendiéndose a la izquierda de −3 y a la derecha de 3. La gráfica se vería como la que está abajo.
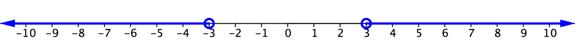
La solución de esta desigualdad puede escribirse: x < −3 o x > 3.
Resolver Desigualdades con Valor Absoluto
Para cualquier valor positivo de a:
x puede ser una variable o una expresión algebraica.
|
Resolver la desigualdad:
A) p ≤ −5 o p ≥ 5
B) −5 ≤ p ≤ 5
C) p ≤ −5
D) No hay solución
|
Veamos algunos ejemplos de desigualdades que contienen valores absolutos.
Ejemplo
| ||||
Problema
|
Resolver x.
| |||
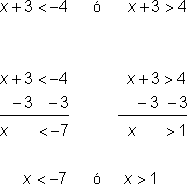 |
Como esta es una desigualdad “mayor que”, la solución puede reescribirse de acuerdo con la regla de “mayor que”. Resuelve cada desigualdad.
| |||
Comprobar
| 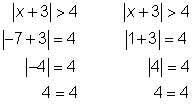 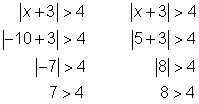 |
Comprueba las soluciones en la ecuación original para asegurarte que son correctas. Comprueba el punto final de la primera ecuación relacionada, −7.
Intenta con −10, un valor menor que −7, para comprobar la desigualdad.
Comprueba el punto final de la segunda ecuación relacionada, 1.
Intenta con 5, un valor mayor que 1.
¡Ambas soluciones funcionan!
| ||
Respuesta
| ||||
Ejemplo
| |||
Problema
|
Resolver y.
| ||
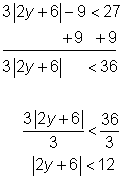 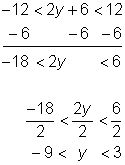 |
Empieza por despejar el valor absoluto sumando 9 a ambos lados de la desigualdad.
Divide entre 3 ambos lados para despejar el valor absoluto.
Escribe la desigualdad de valor absoluto usando la regla “menor que”.
Resta 6 de cada parte de la desigualdad.
Divide entre 2 para despejar la variable.
| ||
Respuesta
| |||
De la misma forma que con las ecuaciones, puede haber ocasiones en las que no hay una solución para una desigualdad.
Ejemplo
| ||||
Problema
|
Resolver x.
|2x + 3| + 9 ≤ 7
| |||
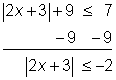 |
Despeja el valor absoluto restando 9 de ambos lados de la desigualdad.
El valor absoluto de una cantidad nunca es un número negativo, por lo que la desigualdad no tiene solución.
| |||
Respuesta
|
No hay solución
| |||
Sumario 😔😝😠😋😑
Para resolver una ecuación que contiene un valor absoluto, debe despejar la expresión que contiene el valor absoluto. Una vez hecho esto, puedes reescribir la ecuación de valor absoluto como dos ecuaciones, donde uno de los enunciados es igual al valor dentro del valor absoluto a la cantidad positiva en el otro lado de la ecuación y el otro es igual al valor absoluto del valor negativo (u opuesto).
Las desigualdades también pueden contener valores absolutos. Las desigualdades absolutas también pueden resolverse reescribiéndolas usando desigualdades compuestas.Resolver Ecuaciones con Valores Absolutos
Como los valores positivos y negativos tienen un valor absoluto positivo, resolver ecuaciones con valores absolutos significa encontrar la solución para ambos valores positivo y negativo.
Primero veamos un ejemplo básico.
La ecuación dice “el valor absoluto de x es igual a cinco.” La solución es el valor o valores que estás a cinco unidades a partir de 0 en la recta numérica.
Podrías pensar inmediatamente en el 5; que es una solución de la ecuación. Observa que −5 también es una solución porque −5 está a 5 unidades del 0 en la dirección opuesta. Entonces la solución a la ecuación 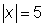 es x = −5 o x = 5.
es x = −5 o x = 5.
Un problema más complejo de valor absoluto se resuelve de manera similar. Considera 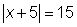 . Esta ecuación te pide encontrar qué número mas 5 tiene un valor absoluto de 15. Como 15 y −15 tienen valor absoluto de 15, la ecuación de valor absoluto es válida cuando la cantidad x + 5 es 15 o x + 5 es −15, ya que |15| = 15 y |−15| = 15. Entonces, necesitas encontrar qué valor de x hará la expresión igual a 15 así como qué valor de x hará la expresión igual a −15. Resolviendo las dos ecuaciones obtienes:
. Esta ecuación te pide encontrar qué número mas 5 tiene un valor absoluto de 15. Como 15 y −15 tienen valor absoluto de 15, la ecuación de valor absoluto es válida cuando la cantidad x + 5 es 15 o x + 5 es −15, ya que |15| = 15 y |−15| = 15. Entonces, necesitas encontrar qué valor de x hará la expresión igual a 15 así como qué valor de x hará la expresión igual a −15. Resolviendo las dos ecuaciones obtienes:
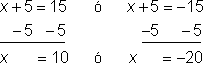
Puedes comprobar ambas soluciones en la ecuación de valor absoluto para ver si x = 10 y x = −20 son correctos.
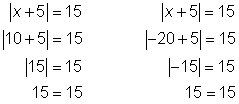
Resolver Ecuaciones de la Forma |x| = a
Para cualquier número positivo a, la solución de |x| = a es
x = a o x = −a
x puede ser una variable o una expresión algebraica.
|
Veamos otro ejemplo.
Ejemplo
| ||||
Problema
|
Resolver p.
|2p – 4| = 26
| |||
Escribe las dos ecuaciones que te darán un valor absoluto de 26.
| ||||
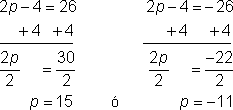 |
Resuelve cada ecuación para p despejando la variable.
| |||
Comprobar | 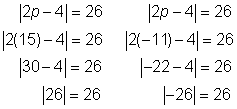 |
Comprueba las soluciones en la ecuación original.
¡Ambas soluciones funcionan!
| ||
Respuesta
| ||||
Algunas veces, tienes que despejar el valor absoluto antes de resolver la ecuación. Un ejemplo se muestra abajo.
Ejemplo
| |||||
Problema
|
Resolver w.
3|4w – 1| – 5 = 10
| ||||
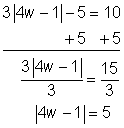 |
Despeja el término con el valor absoluto sumando 5 a ambos lados.
Divide ambos lados entre 3.
Ahora el valor absoluto está despejado.
| ||||
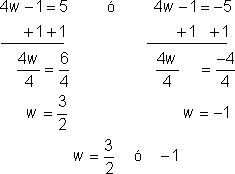 |
Escribe las dos ecuaciones que te darán un valor absoluto de 5 y resuélvelas.
| ||||
Comprobar
| 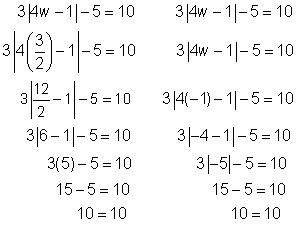 |
Comprueba las soluciones en la ecuación original.
¡Ambas soluciones funcionan!
| |||
Respuesta
| |||||
Veamos otro ejemplo:
Resolver y.
Antes de eliminar el signo de valor absoluto y hacer dos ecuaciones, piensa en lo que significa la ecuación. Dice “el valor absoluto de la cantidad 3y menos 5 es igual a −1.” Recuerda que un valor absoluto es la distancia de 0 en la recta numérica, entonces debe ser un número positivo, Como es imposible tener un valor absoluto igual a −1, esta ecuación no tiene solución. No existen valores de y que hagan un enunciado válido. No hay nada que hacer además de saber que la ecuación no tiene soluciones.
Apliquemos lo que ya sabes sobre resolver ecuaciones que contienen valores absolutos y lo que sabes sobre desigualdades para resolver desigualdades que contienen valores absolutos. Empecemos con una desigualdad simple.
La desigualdad dice, “el valor absoluto de x es menor o igual a 4.” Si se te pide resolver x, quieres encontrar los valores de x que están a 4 unidades o menos de 0 en la recta numérica. Podrías empezar imaginando la recta numérica y los valores de x que satisfacen esta ecuación.
4 y −4 están a cuatro unidades del 0, entonces son soluciones. 3 y −3 también son soluciones porque cada uno de estos valores está a menos de cuatro unidades del 0. Al igual que el 1 y el −1, el 0.5 y el −0.5, etc. — hay un número infinito de valores de x que satisfacen la desigualdad.
La gráfica de esta desigualdad tendrá dos círculos cerrados, en 4 y en −4. La distancia entre estos dos círculos en la recta numérica está coloreada de azul porque estos son los valores que satisfacen la ecuación.

La solución se puede escribir de esta manera: −4 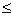 x
x 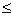 4.
4.
La situación es un poco distinta cuando el signo de desigualdad es “mayor que” o “mayor o igual a.” Considera la desigualdad simple 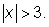 También, podrías pensar en la recta numérica y los valores de x mayores de tres unidades a partir del 0. Esta vez, 3 y −3 no están incluidos en la solución, entonces hay dos círculos abiertos en estos valores. 2 y −2 no serían soluciones porque no están a más de tres unidades del 0. Pero 5 y −5 si están y también lo están todos los valores extendiéndose a la izquierda de −3 y a la derecha de 3. La gráfica se vería como la que está abajo.
También, podrías pensar en la recta numérica y los valores de x mayores de tres unidades a partir del 0. Esta vez, 3 y −3 no están incluidos en la solución, entonces hay dos círculos abiertos en estos valores. 2 y −2 no serían soluciones porque no están a más de tres unidades del 0. Pero 5 y −5 si están y también lo están todos los valores extendiéndose a la izquierda de −3 y a la derecha de 3. La gráfica se vería como la que está abajo.
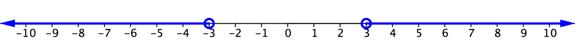
La solución de esta desigualdad puede escribirse: x < −3 o x > 3.
Resolver Desigualdades con Valor Absoluto
Para cualquier valor positivo de a:
x puede ser una variable o una expresión algebraica.
|
Resolver la desigualdad:
A) p ≤ −5 o p ≥ 5
B) −5 ≤ p ≤ 5
C) p ≤ −5
D) No hay solución
|
Veamos algunos ejemplos de desigualdades que contienen valores absolutos.
Ejemplo
| ||||
Problema
|
Resolver x.
| |||
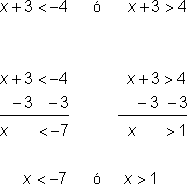 |
Como esta es una desigualdad “mayor que”, la solución puede reescribirse de acuerdo con la regla de “mayor que”. Resuelve cada desigualdad.
| |||
Comprobar
| 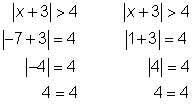 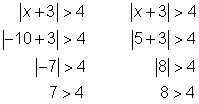 |
Comprueba las soluciones en la ecuación original para asegurarte que son correctas. Comprueba el punto final de la primera ecuación relacionada, −7.
Intenta con −10, un valor menor que −7, para comprobar la desigualdad.
Comprueba el punto final de la segunda ecuación relacionada, 1.
Intenta con 5, un valor mayor que 1.
¡Ambas soluciones funcionan!
| ||
Respuesta
| ||||
Ejemplo
| |||
Problema
|
Resolver y.
| ||
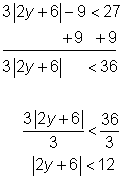 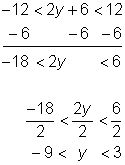 |
Empieza por despejar el valor absoluto sumando 9 a ambos lados de la desigualdad.
Divide entre 3 ambos lados para despejar el valor absoluto.
Escribe la desigualdad de valor absoluto usando la regla “menor que”.
Resta 6 de cada parte de la desigualdad.
Divide entre 2 para despejar la variable.
| ||
Respuesta
| |||
De la misma forma que con las ecuaciones, puede haber ocasiones en las que no hay una solución para una desigualdad.
Ejemplo
| ||||
Problema
|
Resolver x.
|2x + 3| + 9 ≤ 7
| |||
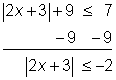 |
Despeja el valor absoluto restando 9 de ambos lados de la desigualdad.
El valor absoluto de una cantidad nunca es un número negativo, por lo que la desigualdad no tiene solución.
| |||
Respuesta
|
No hay solución
| |||
Sumario 😀😡
Para resolver una ecuación que contiene un valor absoluto, debe despejar la expresión que contiene el valor absoluto. Una vez hecho esto, puedes reescribir la ecuación de valor absoluto como dos ecuaciones, donde uno de los enunciados es igual al valor dentro del valor absoluto a la cantidad positiva en el otro lado de la ecuación y el otro es igual al valor absoluto del valor negativo (u opuesto).
Las desigualdades también pueden contener valores absolutos. Las desigualdades absolutas también pueden resolverse reescribiéndolas usando desigualdades compuestas.
Desigualdades Lineales como Regiones 😃😗😖
Las desigualdades lineales son diferentes a las ecuaciones lineales, si bien puedes aplicar lo que sabes sobre ecuaciones para ayudarte a entender las desigualdades. Las desigualdades y las ecuaciones son enunciados matemáticos que comparan dos valores. Las ecuaciones usan el símbolo =; las desigualdades se representan con los símbolos <, ≤, >, y ≥.
Una manera de visualizar desigualdades de dos variables es graficarlas en el plano de coordenadas. Así es como se ve la desigualdad x > y. La solución es la región sombreada.
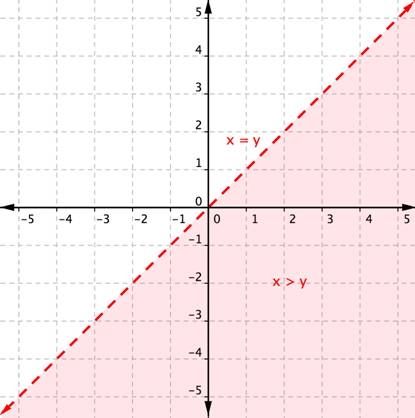
Hay algunas cosas que debemos notar. Primero, observa la recta límite roja y punteada: esta es la gráfica de la ecuación lineal relacionada x = y. Segundo, observa la región roja a la derecha de la recta. Esta región (excluyendo la recta x = y) representa el conjunto de soluciones de la desigualdad x > y. ¿Recuerdas que todos los puntos en la recta son soluciones de la ecuación lineal de una recta? Bueno, todos los puntos en una región son soluciones de la desigualdad lineal que representa esa región.
Pensemos en esto un momento — si x > y, entonces una gráfica de x > y mostrará todos los pares ordenados (x, y) donde la coordenada-x es mayor que la coordenada-y.
La gráfica de abajo muestra la región x > y así como algunos pares ordenados en el plano de coordenadas. Observa cada par ordenado. ¿Es la coordenada-x mayor que la coordenada-y? ¿Está el par ordenado dentro o fuera de la región sombreada?

Los pares ordenados (4, 0) y (0, −3) están dentro de la región sombreada. En estos pares ordenados, la coordenada-x es más grande que la coordenada-y. Estos pares ordenados están en el conjunto solución de la ecuación x > y.
Los pares ordenados (−3, 3) y (2, 3) están fuera de la región sombreada. En estos pares ordenados, la coordenada-x es más pequeña que la coordenada-y, por lo que no están incluidos en el conjunto solución de la desigualdad.
El par ordenado (−2, −2) está en la recta límite. No es una solución porque −2 no es mayor que −2. Sin embargo, si la desigualdad hubiera sido x ≥ y (se lee como “x es mayor o igual que y"), entonces (−2, −2) habría sido incluido (y la recta habría sido representada por una línea sólida, no una línea punteada).
Veamos otro ejemplo: la desigualdad 3x + 2y ≤ 6. LA gráfica siguiente muestra la región de valores que vuelve la desigualdad válida (rojo sombreado), la recta límite 3x + 2y = 6, así como un grupo de pares ordenados. Esta vez, a recta límite es sólida, porque puntos en la recta límite 3x + 2y = 6 también son válidos en la ecuación 3x + 2y ≤ 6.

Como hiciste en el ejemplo anterior, puedes sustituir los valores de x y, y en cada uno de los pares ordenados (x, y), en la desigualdad para encontrar soluciones. Si bien pudiste hacerlo en la mente para la desigualdad x > y, a veces construir una tabla de valores tiene sentido para desigualdades más complicadas.
Par Ordenado
|
Hace a la desigualdad
3 x + 2y ≤ 6
un enunciado válido
|
Hace la desigualdad
3 x + 2y ≤ 6
un enunciado inválido
|
(−5, 5)
|
3(−5) + 2(5) ≤ 6
−15 +10 ≤ 6
−5 ≤ 6
| |
(−2, −2)
|
3(−2) + 2(–2) ≤ 6
−6 + (−4) ≤ 6
–10 ≤ 6
| |
(2, 3)
|
3(2) + 2(3) ≤ 6
6 + 6 ≤ 6
12 ≤ 6
| |
(2, 0)
|
3(2) + 2(0) ≤ 6
6 + 0 ≤ 6
6 ≤ 6
| |
(4, −1)
|
3(4) + 2(−1) ≤ 6
12 + (−2) ≤ 6
10 ≤ 6
|
Si sustituimos (x, y) en la desigualdad y obtenemos un enunciado válido, entonces el par ordenado es una solución de la desigualdad, y el punto estará graficado dentro de la región sombreada o será parte de la recta límite sólida. Un enunciado falso significa que el par ordenado no es una solución, y el punto estará fuera de la región sombreada, o será parte de una recta límite punteada.
No hay comentarios:
Publicar un comentario