Procesos algebraicos

Procesos algebraicos  😥😔😏😔

EXPRESIONES ALGEBRAICAS 😓😖

Una expresión algebraica contiene letras, números y signos. La manipulación de expresiones algebraicas tiene las mismas propiedades que la manipulación de expresiones numéricas, ya que las letras se comportan como si fuesen números. Las expresiones algebraicas que se tratarán en este curso tendrán, por lo general, una o dos letras. Un ejemplo de expresión con una única letra es:

3x2+4x−2−x2+7x$3x^2+4x-2-x^2+7x$

Ante cualquier expresión, lo primero que debe hacerse es simplificarla, utilizando las propiedades de las expresiones, que son equivalentes a las propiedades de los números. En el caso del ejemplo, deben agruparse los términos con las mismas letras. Por un lado, debemos sumar 3x2$3x^2$ y −x2$-x^2$, mientras que, por otro lado, se debe sumar 4x$4x$ y 7x$7x$:

3x2−x2=2x2${3x}^2-x^2=2x^2$

4x+7x=11x$4x+7x=11x$

Así pues, la expresión de segundo grado 3x2+4x−2−x2+7x$x^2+4x-2-x^2+7x$ es igual a 2x2+11x−2${2x}^2+11x-2$.

El valor numérico de una expresión algebraica se halla sustituyendo la letra por un número de terminado. Por ejemplo, el valor numérico de 2x2+11x−${2x}^2+11x-$2 cuando x=3$x=3$ es igual a 2⋅32+11⋅3−2=18+33−2=49.${2·3}^2+11·3-2=18+33-2=49.$

El grado de una expresión algebraica con una única letra es el exponente máximo de esta letra en la expresión. Por ejemplo, el grado de 2x2+11x−${2x}^2+11x-$2 es 2.

PROPIEDADES ALGEBRAICAS   😂😓😠

La Propiedad Conmutativa de la Suma y de la Multiplicación  😟😛😖😌

Te encontrarás con rutinas diarias cuyo orden puede ser intercambiado sin modificar el resultado. Por ejemplo, piensa en servir una taza de café en la mañana. Tendrás la misma taza de café sin importar en qué orden añades los ingredientes:

·         Servir 12 onzas de café en una taza, luego añadir leche.

·         Añadir leche en una taza, luego añadir 12 onzas de café.

El orden en el que añades los ingredientes no importa. De la misma manera, no importa si te pones primero el zapato izquierdo o si te pones primero el zapato derecho para ir a trabajar. Siempre y cuando traigas puestos los dos zapatos al salir de tu casa, ¡todo saldrá bien!

En las matemáticas, decimos que estas situaciones son conmutativas — el resultado será el mismo (el café se prepara a tu gusto; sales de tu casa con ambos zapatos puestos) sin importar el orden en el que se realizan las tareas.

Igualmente, la propiedad conmutativa de la suma dice que cuando dos números son sumados, el orden puede ser cambiado sin afectar el resultado. Por ejemplo, 30 + 25 da el mismo resultado que 25 + 30.

30 + 25 = 55

25 + 30 = 55

La multiplicación se comporta de la misma forma. La propiedad conmutativa de la multiplicación dice que cuando dos números se multiplican, su orden puede cambiar sin afectar el resultado. Por ejemplo, 7 · 12 tiene el mismo producto que 12 · 7.

7 · 12 = 84

12 · 7 = 84

Estas propiedades se aplican a todos los número reales. Echemos un vistazo a algunos ejemplos de suma.

Ecuación Original	Ecuación reescrita
1.2 + 3.8 = 5	3.8 + 1.2 = 5
14 + (−10) = 4	(−10) + 14 = 4
(−5.2) + (−3.6) = −8.8	(−3.6) + (−5.2) = −8.8

Propiedad Conmutativa de la Suma

Para cualesquiera números reales a y b, a + b = b + a.

La resta no es conmutativa. Por ejemplo, 4 − 7 no tiene la misma diferencia que 7 − 4. Aquí, el signo − significa resta.

Sin embargo, recuerda que 4 − 7 puede reescribirse como 4 + (−7), porque restar un número es lo mismo que sumar su opuesto. Aplicando la propiedad conmutativa de la suma, puedes decir que 4 + (−7) es lo mismo que (−7) + 4. Observa cómo esta expresión es muy distinta a 7 – 4.

Ahora veamos algunos ejemplos de multiplicación.

Ecuación Original	Ecuación Reescrita
4.5 · 2 = 9	2 · 4.5 = 9
(−5) · 3 = -15	3 · (−5) = -15

Propiedad Conmutativa de la Multiplicación

Para cualesquiera números reales a y b, a · b = b · a.

El orden no importa siempre y cuando las dos cantidades se multipliquen. Esta propiedad funciona para números reales y para variables que representen números reales.

De la misma forma que la resta, la división tampoco es conmutativa. 4 ÷ 2 no tiene el mismo cociente que 2 ÷ 4.

Ejemplo
Problema	Reescribe la expresión (−15.5) + 35.5 de una manera distinta, usando la propiedad conmutativa de la suma, y muestra que ambas expresiones dan el mismo resultado.
(−15.5) + 35.5 = 20   35.5 + (−15.5)   35.5 + (−15.5)   35.5 – 15.5 = 20		Sumando. Usando la propiedad conmutativa, puedes cambiar el −15.5 y el 35.5 para que queden en orden distinto. Sumar 35.5 y −15.5 es lo mismo que restar 15.5 de 35.5. La suma es 20.
Respuesta        (−15.5) + 35.5 = 20 y 35.5 + (−15.5) = 20

Reescribe 52 • y de una manera distinta, usando la propiedad conmutativa de la multiplicación. Ten en cuenta que y representa un número real. A) 5y • 2 B) 52y C) 26 • 2 • y D) y • 52 Mostrar/Ocultar Respuesta

Las Propiedades Asociativas de la Suma y de la Multiplicación  😠😜😞

La propiedad asociativa de la suma dice que los números en una expresión aditiva pueden agruparse de distinta manera sin cambiar la suma. Puedes recordar el significado de la propiedad asociativa recordando que cuando te asocias con familiares, amigos, y compañeros, formas grupos con ellos.

Abajo hay dos maneras de simplificar el mismo problema de suma. En el primer ejemplo, el 4 se agrupa con el 5, y 4 + 5 = 9.

4 + 5 + 6 = 9 + 6 = 15

Aquí, en el mismo problema, primero se agrupan el 5 y el 6, 5 + 6 = 11.

4 + 5 + 6 = 4 + 11 = 15

En ambos casos, la suma es la misma. Esto ilustra que cambiar el agrupamiento de números que se suman resulta en el mismo número.

Los matemáticos normalmente usan paréntesis para indicar qué operación debe realizarse primero en una ecuación algebraica. Los problemas de suma de arriba se reescriben, esta vez usando paréntesis para indicar su agrupamiento asociativo.

(4 + 5) + 6 = 9 + 6 = 15

4 + (5 + 6) = 4 + 11 = 15

Es claro que los paréntesis no afectan la suma; la suma sigue siendo la misma a pesar de que se han incluido paréntesis.

Propiedad Asociativa de la Suma

Para cualesquiera números reales a, b, y c, (a + b) + c = a + (b + c).

El ejemplo de abajo muestra cómo se aplica la propiedad asociativa para simplificar expresiones con números reales.

Ejemplo
Problema		Reescribe 7 + 2 + 8.5 – 3.5 de una manera distinta, usando la propiedad asociativa de la suma, y muestra que ambas expresiones dan el mismo resultado.
7 + 2 + 8.5 – 3.5 7 + 2 + 8.5 + (−3.5)				La propiedad asociativa no aplica a las expresiones de resta. Entonces, reescribe la expresión como la suma de un número negativo.
(7 + 2) + 8.5 + (−3.5)   9   + 8.5 + (−3.5)       17.5 + (−3.5)       17.5 – 3.5 = 14				Agrupa 7 y 2, y súmalos. Luego, súmales 8.5. Finalmente, suma −3.5, que es lo mismo que restar 3.5. Resta 3.5. La suma es 14.
7 + 2 + (8.5 + (−3.5)) 7 + 2 +     5   9  +     5 14				Agrupa 8.5 y –3.5, y luego súmalos para obtener 5. Luego suma 7 y 2, y súmalos al 5. La suma es 14.
Respuesta    (7 + 2) + 8.5 – 3.5 = 14 y 7 + 2 + (8.5 + (−3.5)) = 14

La multiplicación tiene una propiedad asociativa que funciona exactamente igual que la de la suma. La propiedad asociativa de la multiplicación dice que los números en una expresión de multiplicación pueden reagruparse usando paréntesis. Por ejemplo, la expresión siguiente puede ser reescrita de dos maneras distintas usando la propiedad asociativa.

Expresión original: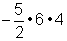 

Expresión 1: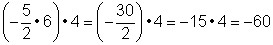 

Expresión 2: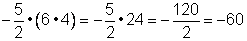 

el paréntesis no afecta el producto, el producto es el mismo sin importar en dónde están los paréntesis.

Propiedad Asociativa de la Multiplicación

Para cualesquiera números reales a, b, y c, (a • b) • c = a • (b • c).

Reescribe  usando la propiedad asociativa. A)  B)  C)  D)  Mostrar/Ocultar Respuesta

Usando las Propiedades Asociativa y Conmutativa    😌😓😍

Encontrarás que las propiedades asociativa y conmutativa son herramientas útiles en el álgebra, especialmente cuando tienes que evaluar expresiones. Usando las propiedades conmutativa y asociativa, puedes re ordenar los términos en una expresión para que números compatibles queden uno junto al otro y agrupados. Los números compatibles son números que son fáciles de calcular, como 5 + 5, o 3 ·10, o 12 – 2, o 100 ÷ 20. (El criterio principal para números compatibles es que “funcionan bien” juntos.) Los dos ejemplos siguientes muestran cómo se hace.

Ejemplo
Problema		Evalúa la expresión 4 · (x · 27) cuando .
				Expresión original. Sustituir  por x. Usa la propiedad asociativa de la multiplicación para reagrupar los factores de tal forma que 4 y  queden juntos. Multiplicar 4 por  primero, hace que la expresión sea más fácil de evaluar, en lugar de multiplicar  por 27. Multiplica. 4 veces  = −3, y −3 veces 27 es −81.
Respuesta     cuando .

Ejemplo
Problema			Simplifica: 4 + 12 + 3 + 4 – 8.
4 + 12 + 3 + 4 – 8 12 + 3 + 4 + 4 + (−8) 12 + 3 + (4 + 4 + (−8)) 12 + 3 + 0 12 + 3 + 0 = 15					Expresión original. Identifica los números compatibles. 4 + 4 es 8, y hay un −8. Recuerda que puedes pensar en el – 8 como + (−8). Usa la propiedad conmutativa de la suma para agruparlos juntos. Usa la propiedad asociativa para agrupar 4 + 4 + (−8). Suma 4 + 4 + (−8). Suma el resto de los términos.
		Respuesta       4 + 12 + 3 + 4 – 8 = 15

Simplifica la expresión: −5 + 25 – 15 + 2 + 8 A) 5 B) 15 C) 30 D) 55 Mostrar/Ocultar Respuesta

La Propiedad Distributiva    😞😛😔

La propiedad distributiva de la multiplicación es una propiedad muy útil que nos permite reescribir expresiones en las que estás multiplicando un número por una suma o una resta. La propiedad dice que el producto de una suma o una resta como 6(5 – 2), es igual a la suma o resta de los productos, en este caso, 6(5) – 6(2).

                                    6(5 – 2) = 6(3) = 18

                                    6(5) – 6(2) = 30 – 12 = 18

La propiedad distributiva de la multiplicación puede usarse cuando multiplicas un número por una suma. Por ejemplo, supón que quieres multiplicar 3 por la suma de 10 + 2.

3(10 + 2) = ?

de acuerdo con esta propiedad, puedes sumar los número 10 y 12 primero y luego multiplicar por 3, como se muestra aquí: 3(10 + 2) = 3(12) = 36. de manera alternativa, puedes multiplicar cada sumando por tres (a esto se le llama distribuir el 3), y luego puedes sumar los productos. El proceso se muestra a continuación.

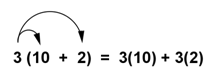
3 (10 + 2) = 3(12) = 36

3(10) + 3(2) = 30 + 6 = 36

Los productos son iguales.

Como la multiplicación es conmutativa, puedes usar la propiedad distributiva sin importar el orden de los factores.

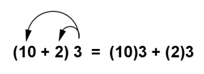
Las Propiedades Distributivas

Para cualesquiera números reales a, b, y c:

La multiplicación se distribuye sobre la suma:      a(b + c) = ab + ac

La multiplicación se distribuye sobre la resta:       a(b – c) = ab – ac

Reescribe la expresión 10(9 – 6) usando la propiedad distributiva. A) 10(6) – 10(9) B) 10(3) C) 10(6 – 9) D) 10(9) – 10(6) Mostrar/Ocultar Respuesta

Distribuyendo con Variables   😒😕😐

Siempre y cuando las variables representen números reales, la propiedad distributiva puede usarse con ellas. La propiedad distributiva es importante en el álgebra, y muchas veces verás expresiones como esta: 3(x – 5). Si se te pide expandir la expresión, puedes aplicar la propiedad distributiva de la misma forma que lo harías con enteros.

3 (x – 5 ) = 3(x) – 3(5) = 3x – 15

Recuerda, cuando multiplicas un número por una variable, puede escribirlos uno junto al otro para expresar que se están multiplicando. Entonces, la expresión “tres veces la variable x” se puede escribir de varias formas: 3x, 3(x), o 3 · x.

Ejemplo
Problema	Usa la propiedad distributiva para expandir la expresión 9(4 + x).
9(4 + x) 9(4) + 9(x) 36 + 9x		Expresión original. Distribuye el 9 y multiplica. Multiplica.
Respuesta   9(4 + x) = 36 + 9x

Ejemplo
Problema	Usa la propiedad distributiva para expandir la expresión 5(2x – 3) cuando x = 2.
5(2x – 3)  5(2x) – 5(3) 10x – 15 10(2) – 15 20 – 15 = 5		Expresión original. Distribuye el 5. Multiplica. Sustituye 2 por x, y evalúa.
Respuesta   Cuando x = 2, 5(2x – 3) = 5.

En el ejemplo anterior, ¿qué crees que pasaría si sustituyes x = 2 antes de distribuir el ? ¿Obtendrías el mismo resultado de 5? El ejemplo siguiente muestra lo que pasaría.

Ejemplo
Problema	Usa la propiedad distributiva para expandir la expresión 5(2x – 3) cuando x = 2.
5(2x – 3) 5(2(2) – 3) 5(4 – 3) 5(4) – 5(3) 20 – 15 = 5		Expresión original. Sustituye 2 por x. Multiplica. Resta y evalúa.
Respuesta   Cuando x = 2, 5(2x – 3) = 5.

Combinando Términos Semejantes   😟😝😖

La propiedad distributiva también puede ayudar a entender una idea fundamental en el álgebra: que cantidades como 3x y 12x pueden sumarse y restarse de la misma manera que los números 3 y 12. Veamos un ejemplo para ver cómo se hace esto.

Ejemplo
Problema	Suma: 3x + 12x.
3(x) + 12(x) x(3 + 12) x(15) o 15x		3x es 3 veces x, y 12x es 12 veces x. De estudiar la propiedad distributiva (y también usando la propiedad conmutativa, sabes que x(3 + 12) es lo mismo que 3(x) + 12(x). Combina los términos dentro de los paréntesis: 3 + 12 = 15.
Respuesta   3x + 12x = 15x

¿Viste lo que pasó? Si penamos que x es una cantidad distribuida, puedes ver que 3x + 12x = 15x. (Si no estás seguro de ello, intenta sustituir cualquier número por x en la expresión... encontrarás que siempre es válido!)

Los grupos de términos que consisten en un coeficiente multiplicado por la misma variable se llaman “términos semejantes”. La tabla siguiente muestra algunos grupos diferentes de términos semejantes:

Grupos de Términos Semejantes

3x, 7x, −8x, −0.5x

−1.1y, −4y, −8y

12t, 25t, 100t, 1t

4ab, −8ab, 2ab

Siempre que ves términos semejantes en una expresión algebraica o una ecuación, puedes sumarlos o restarlos como lo harías con números reales. Por ejemplo,

10y + 12y = 22y, y 8x – 3x – 2x = 3x.

Ten cuidado de no combinar términos que no tienen la misma variable: ¡4x + 2y no es 6xy!

Ejemplo
Problema	Simplifica: 10y + 5y + 9x – 6x – x.
10y + 5y + 9x – 6x – x 15y   +   2x		Hay términos semejantes en esta expresión, porque todos son un coeficiente multiplicado por una variable xo y. Observa que – x es lo mismo que (−1)x. Suma los términos semejantes. 10y + 5y = 15y, y 9x – 6x – x = 2x.
Respuesta      10y + 5y + 9x – 6x – x = 15y + 2x

Simplifica: 12x – x + 2x – 8x. A) 23x B) 5 C) 5x D) x Mostrar/Ocultar Respuesta

Sumario  😝😞😖😗

Las propiedades conmutativa, asociativa, y distributiva nos ayudan a reescribir expresiones algebraicas complicadas a otras más fáciles de entender. Cuando reescribes una expresión usando la propiedad conmutativa, cambias el orden de los números que están siendo sumados o multiplicados. Cuando reescribes una expresión usando la propiedad asociativa, agrupas pares distintos de números usando paréntesis. Puedes usar las propiedades conmutativa y asociativa para reagrupar y ordenar cualquier número en una expresión siempre y cuando la expresión esté hecha enteramente de sumandos o factores (y no una combinación de ellos). La propiedad distributiva puede usarse para reescribir expresiones con varios propósitos. Cuando estás multiplicando un número por una suma, puedes sumar y luego multiplicar. También puedes multiplicar primero cada sumando y luego sumar los producto. Aplica el mismo principio si estás multiplicando un número por una diferencia.

MONOMIOS, BINOMIOS Y POLINOMIOS  😱😝😟

Un monomio es cualquier producto de números y variables, como 17, o 3 xy , o –4 x 2 , o

Las únicas reglas son que las variables deben ser elevadas únicamente a las potencias de enteros positivos (no se permiten raíces cuadradas o 1/ x ), y no se permiten signos de más o menos.

Un binomio es la suma de dos monomios, por ejemplo x + 3, o 55 x 2 – 33 y 2 , o

Un trinomio es la suma de tres monomios.

Un polinomio es la suma de n monomios, para algún número entero n . Así los monomios, binomios y trinomios todos son casos especiales de polinomios. Un polinomio puede tener tantos términos como Usted desee.